GA (Genetic Algorithm)
개인적 해석
- 최적의 해를 찾는 알고리즘이라고 생각함 Ex. Cost 최소화, 이익 최대화
- GA가 정확하고, 최적의 값을 찾기 위해서는 모델의 정당성, 신뢰도가 확보되어야 함
- 부모 염색체가 정확하지 않은 값이라면 당연히 자손 염색체도 좋은 결과 값이 나올 수 없다고 생각함
- Fitness function을 얼마나 창의적으로 설계하느냐가 GA의 핵심이라는 생각이 듦
의미
- 최적의 해를 구하는 방법론인 GA라고 불리는 유전 알고리즘
- 지도학습, 비지도학습이라고 오해할 수 있지만 GA는 모델의 종류가 아닌 파라미터의 최적화 문제를 풀기 위한 일종의 방법
개념 정의
- 염색체(Chromosome) : 여러개의 유전자를 담고 있는 하나의 집합을 의미한다. GA에서는 하나의 해(파라미터)를 표현한다.
- 유전자(Gene) : 염색체를 구성하고 있는 요소로서, 하나의 유전 정보를 나타낸다. 예를 들어, 하나의 특정한 염색체가 [A,B,C,D] 라고 정의된다면 해당 염색체의 유전자는 A,B,C,D로 4개의 유전자가 존재한다.
- 자손(Offspring) : 특정 시간(t)에 존재했던 염색체들(예를 들어, A,B 두 개의 염색체가 있다고 가정.)로부터 생성된 새로운 염색체들(C,D라고 가정.)이다. 즉 C,D 는 A,B 염색체들의 자손이라고 할 수 있다. 자손 염색체는 부모 염색체의 비슷한 유전 정보를 갖는다.
- 정확도(Fitness) : 특정한 염색체가 갖고 있는 고윳값으로서, 특정한 염색체가 표현하는 해(파라미터)가 해결하려는 문제에 대해 얼마나 적합한지를 나타낸다.
연산정의
초기에 어떠한 문제에 적용하기 위해서 총 5개의 연산을 정의해야함.
- 초기 염색체를 생성하는 연산
- 최초의 염색체를 생성하기 위해서는 이전의 염색체가 존재하지 않기 때문에 최초의 염색체를 생성하는 연산을 따로 정의해주어야 한다. GA에서 가장 많이 이용되는 방법은 규칙 없이 임의의 값으로 초기 염색체를 생성하는 것이다.
- 적합도를 계산하는 연산
- 염색체에 표현된 정보를 토대로 적합도를 계산하는 연산이다. 이 연산은 해결하려는 문제에 따라 달라진다.
- 적합도를 기준으로 염색체를 선택하는 연산
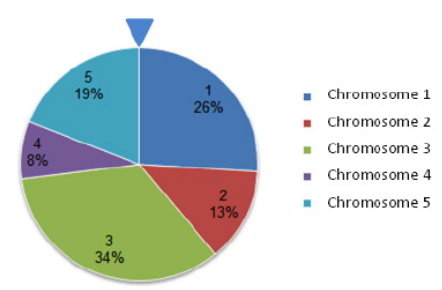
- 자손 염색체를 생성할 때 흔히 적합도가 가장 높은 염색체들을 선택하는 것이 최고의 방법이라고 생각할 수 있다. 하지만 이러한 방법은 염색체의 다양성을 손상시키기 때문에 Global optimum을 찾기에는 부적합하다. 이러한 문제를 피하기 위해서 GA에서는 룰렛 휠 선택(Roulette Wheel Selection) 방법을 이용한다. 룰렛 휠 선택이란, 우리가 흔히 생각하는 원판을 돌리면서 확률에 기반해 결과가 도출되는 룰렛의 개념과 비슷하다고 생각하면 된다. 밑의 그림은 룰렛 휠 선택에 대한 확률적 수식이며 다음 그림은 수식을 룰렛 그림으로 나타낸 그림이다. 룰렛 그림에서 면적의 총 합은 1(100%)이다. 왜냐하면 각각이 확률값이며 확률의 합은 1이기 때문이다.
- 선택된 염색체들로부터 자손을 생성하는 연산
- 방금 언급했던 룰렛 휠 선택 방법으로 선정된 두 개의 부모 염색체들로부터 하나의 자손 염색체를 생성한다. 이 때 GA에서는 자손 염색체를 생성하는 연산으로서 주로 Crossover이라는 연산을 사용한다. Crossover 연산에 대해 그림으로 설명하자면 다음과 같다.
- 돌연변이 (mutation) 연산
- 룰렛 휠 선택을 통해 Crossover 연산만을 사용한다면 Local optimum에 빠지는 문제를 발생시킬 수 있다. 이러한 문제를 피하기 위해서 자손 염색체에 돌연변이 연산을 추가적으로 적용하는 방법이 있다.
- 보통은 0.1%나 0.05%등의 아주 낮은 확률로 돌연변이가 발생하도록 한다.
알고리즘 구조
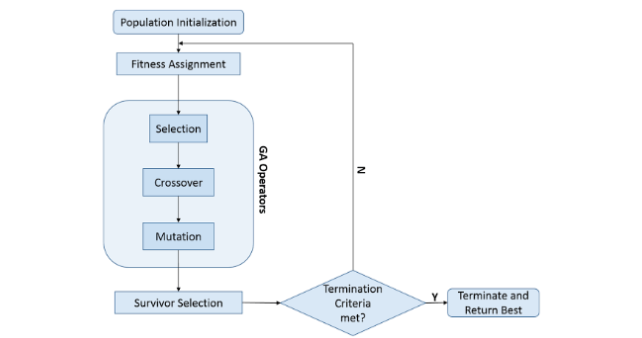
유전 알고리즘은 t에 존재하는 염색체들의 집합으로부터 적합도가 가장 좋은 염색체를 선택하고, 선택된 해의 방향으로 검색을 반복하면서 최적해를 찾아가는 구조로 동작한다.
- 초기 염색체의 집합 생성
- 초기 염색체들에 대한 적합도 계산
- 현재 염색체들로부터 자손들을 생성
- 생성된 자손들의 적합도 계산
- 종료 조건 판별
6-1) 종료 조건이 거짓인 경우, (3)으로 이동하여 반복
6-2) 종료 조건이 참인 경우, 알고리즘을 종료
Fitness Function
- 일반적으로 지도학습을 사용하는 분류 작업의 경우 유클리드 거리 및 맨해튼 거리와 같은 오류 측정이 피트니스 함수로 널리 알려져서 사용되어 왔음.
- 최적화 문제의 경우 문제 영역과 관련된 계산, 매개 변수 집합의 합과 같은 기본기능을 피트니스 함수로 사용할 수 있음